Benjamin Mossé

© 2025. All rights reserved.

How We Know What's Real: Deutsch's Criterion for Reality

14 Nov 2025

How can we know what’s real or not? That’s the key question David Deutsch sets out to answer in Chapter 4 of The Fabric of Reality (TFoR).

David offers logical refutations for the recurring errors found in theories that claim to describe reality. He then explains a positive criterion for deciding what is real.

Reality’s Simplest Test

A simple but powerful way to expose ideas that don’t match reality: show that they don’t actually solve the problem they claim to solve.

David Deutsch gives the example of the Catholic Inquisition forcing Galileo to recant his support for heliocentrism, insisting instead on the Ptolemaic geocentric model.

Deutsch points out that if the Inquisition had taken their own theory seriously, they would’ve seen it couldn’t explain the planetary motions they observed in the sky.

They had no coherent answers to questions such as:

Every unexplained observation forced them to bolt on new, ad-hoc complications.

The key attribute, Deutsch argues, is that good explanations are hard-to-vary: change any part, and it stops explaining the phenomena.

Bad explanations, on the other hand, are easy-to-vary and stay alive only through arbitrary patches.

Testing a theory using this method is simple:

  1. List the problems the theory claims to solve
  2. List the phenomena it must explain
  3. Verify whether it explains the phenomena and solves the problems without bolting on new complexities that demand even more explanation
  4. If it doesn’t, then discard the theory

Refuting all forms of Solipsism

David then turns to what he calls “solipsistic” theories.

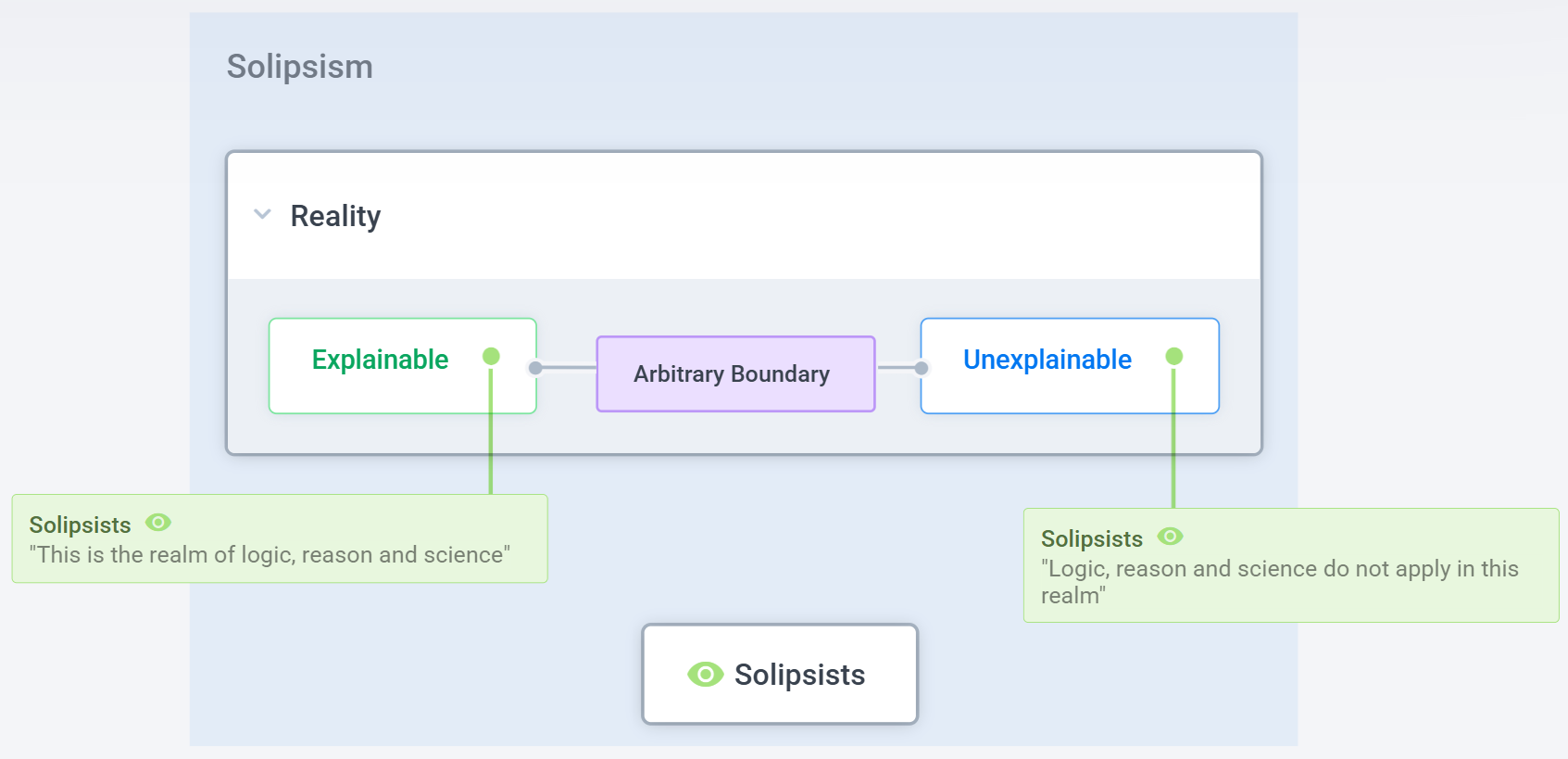
In philosophy, solipsism is the claim that only one’s own mind is certain to exist. But Deutsch uses the term more broadly.

For him, a theory is “solipsistic” if it draws an arbitrary boundary on what can be known or explained, claiming that beyond a certain point reason and problem-solving cannot reach.

In other words, any theory that says “this part of reality is off-limits to explanation” falls into his expanded definition of solipsism.

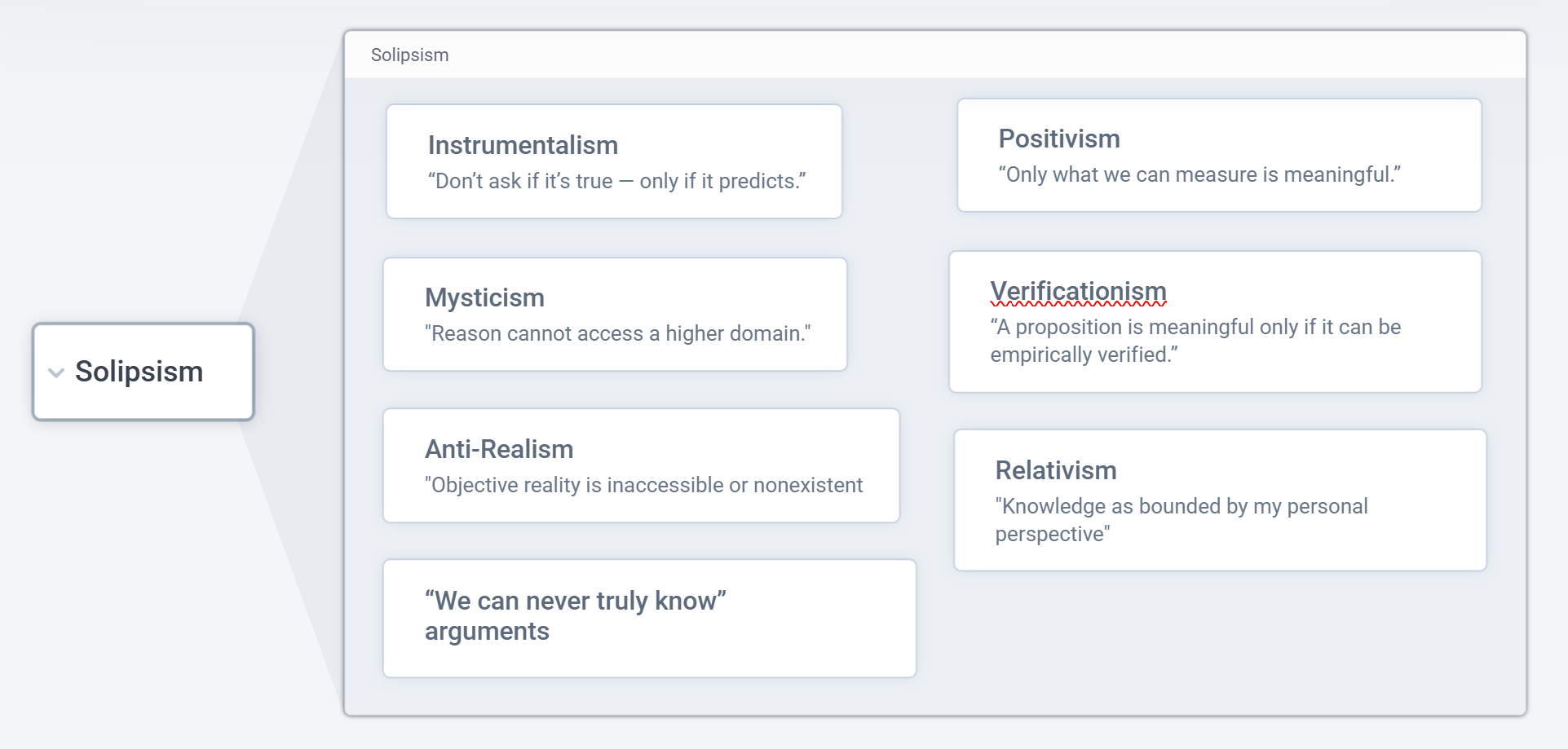
Here’s a diagram I created that shows a non-exhaustive list of solipsistic theories as per David’s definition:

David then shows that solipsism (in all its forms) fails because it offers no additional explanatory power.

A solipsist who claims that only his own mind exists still has to explain why his experiences behave in ways that can be described and understood. He must explain how his mind produces planet-like experiences that follow laws-of-physics-like patterns, and then justify why adding a mind parameter explains those patterns better than the straightforward explanations that do not require it.

Supernatural theories face the same problem: they must explain everything that natural theories already explain and then show why the supernatural element adds genuine explanatory power.

In short, solipsism is realism with extra complications, and therefore an inferior explanation.

Refuting Ultimate Sources of Justification

For millennia, humans have searched for an ultimate source of justification. A book, a story, an authority, a method, something that would explain everything they saw and experienced.

David shows that this hope is futile, because “explanations are not justified by the means by which they were derived; they are justified by their superior ability, relative to rival explanations, to solve the problems they address” (p. 84).

He also argues that “a prediction, or any assertion, that cannot be defended might still be true, but an explanation that cannot be defended is not an explanation” (p. 85).

A key takeaway is that there is no hierarchy of reliability for producing good explanations. Mathematics is not inherently superior to philosophy, nor is philosophy superior to the scientific method.

What we really need, David continues, is to “develop reasons for accepting or rejecting the existence of entities that may appear in contending theories; in other words, we need a criterion for reality” (p. 85).

The Criteria for Reality

And so we finally arrive at the goal of the chapter, which is to offer a criterion for reality.

The first advice David gives is to abandon the idea that such a criterion can ever be finite.

He writes, “not only do explanations change, but our criteria and ideas about what should count as an explanation are gradually changing (improving too). So the list of acceptable modes of explanation will always be open-ended, and consequently the list of acceptable criteria for reality must be open-ended too” (p. 86).

But what should the criterion be for classifying things as real or imaginary?

Before discussing the criterion, it is useful to recall some general ideas from Popperian epistemology that help us evaluate competing explanations, such as problem solving, explanatory power, hard to vary structure, and the ability to make testable predictions.

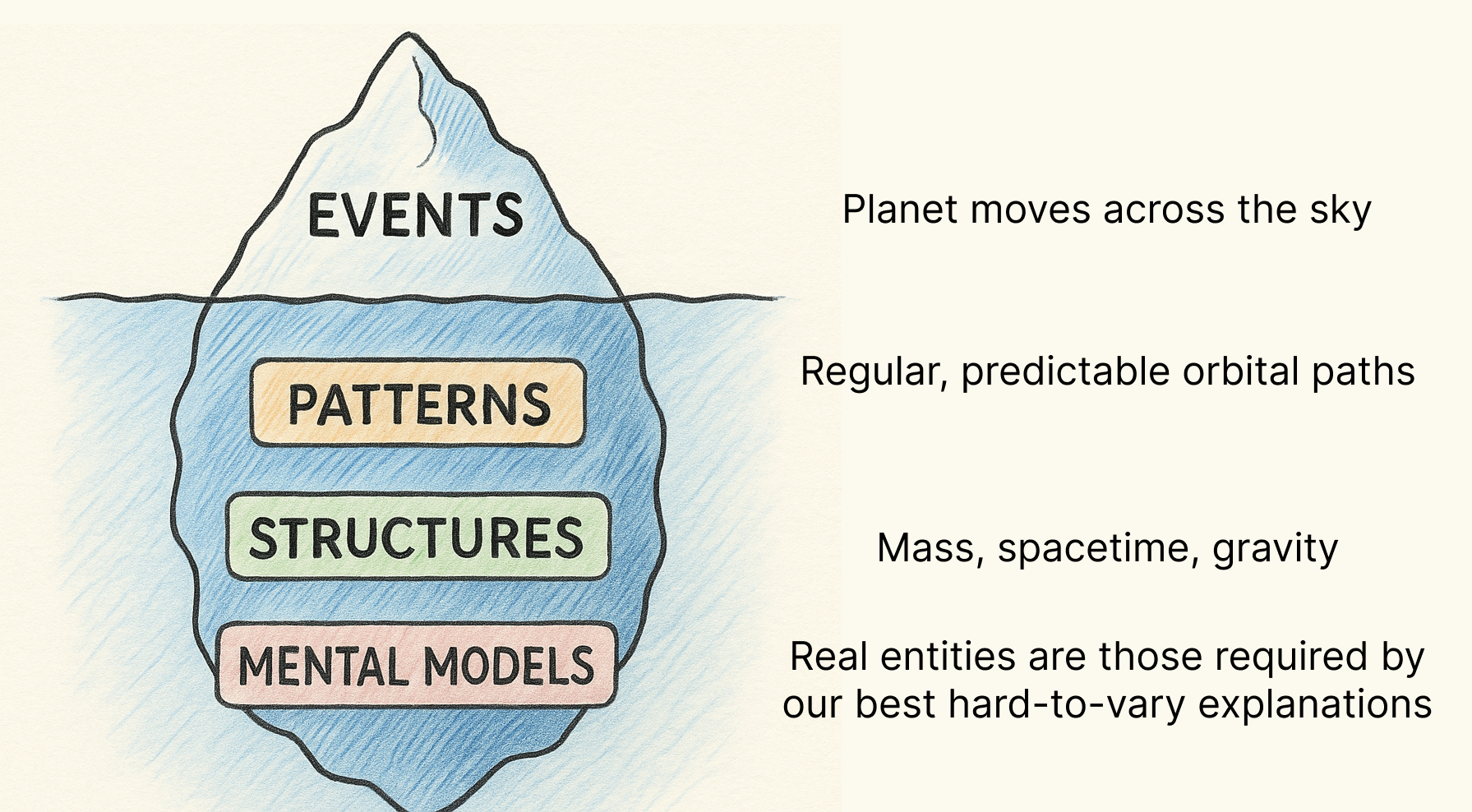
Now imagine you have compared several competing theories and chosen the most powerful one relative to its rivals. David explains, “if, according to the simplest explanation, an entity is complex and autonomous, then that entity is real” (p. 91).

When the best explanation requires an entity to be complex and autonomous, we should regard that entity as real.

“Complex” means the entity contributes something the explanation cannot do without (i.e., the mass of the electron or a particular gene sequence). Change its properties, and the explanation collapses.

This matters because only real entities place constraints on what is possible; only real entities can do things independently of our descriptions or expectations.

This connects what we can explain with what we should regard as real, connecting epistemology and ontology.

Conversely, entities such as phlogiston, the ether, vital forces, or epicycles are unreal because no explanation depends on them. Removing them does not reduce explanatory power, and therefore they are redundant rather than complex and autonomous.

For example, to explain and predict the motion of the planets in the solar system, we need a theory such as General Relativity, which consists of ten field equations that can be written in a single compact form:

I do not understand the mathematics of General Relativity, but what we have here is a hard to vary equation that accounts for a vast range of the macroscopic structure of the universe.

It explains a remarkable amount of complexity and shows why planets and stars move in autonomous ways.

We can also use it to simulate parts of the universe, and each simulation requires substantial computation.

The internal structure of General Relativity predicted black holes long before they were observed experimentally.

Further Explaining Autonomy

There is more to this chapter, but I want to note one final idea that David emphasizes: “reality will respond with evidence if we interact appropriately with it” (p. 94).

In other words, if something reliably “kicks back” when we test it, then it exists.

This is the practical expression of autonomy: if an entity can push back against our attempts to explain or manipulate it, then it is real.

Conclusion

All of this, taken together, introduces criterion to justify:

These entities are real not because we can observe them directly, but because our best explanations cannot function without them.

Reality is what our best explanations require to exist, not just what we can directly observe.

Thank you for reading. If any errors or misunderstandings appear in this article, they are entirely my own and should not be attributed to David Deutsch or his work.